Implementation

Implementation

Keling, Dijkstra algoritmini kodda qanday amalga oshirishni ko'rib chiqaylik. Mana misol uchun men foydalanadigan grafik.

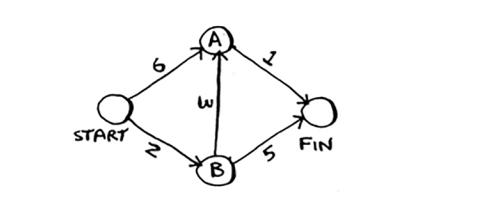
Ushbu misolni kodlash uchun sizga uchta hash-jadval kerak bo'ladi.

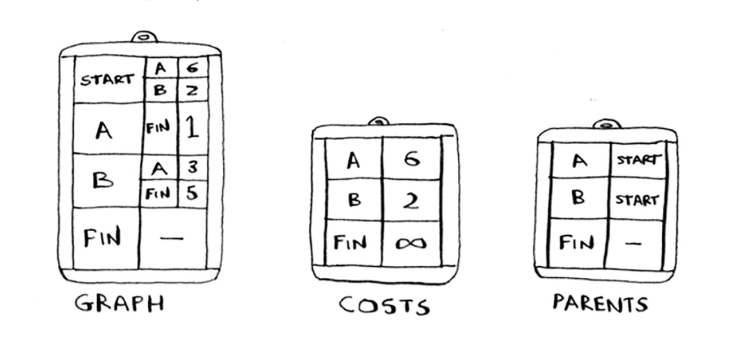
Algoritm rivojlanishi bilan siz xarajatlar va ota-onalarning xesh jadvallarini yangilaysiz. Birinchidan, siz grafikni amalga oshirishingiz kerak. Siz 6-bobdagi kabi xesh jadvalidan foydalanasiz:

Python

grafik = {}

Golang

grafik := make(map[string]map[string]int)

Oxirgi bobda siz tugunning barcha qo'shnilarini xesh jadvalida saqladingiz, masalan:

Python

grafik ["you"] = ["alisa", "bob", "claire"]

Golang

grafik["you"] = map[string]int{"alisa": 2, "bob": 2, "claire": 5}

Ammo bu safar siz qo'shnilarni saqlashingiz kerak va qo'shniga borish xarajatlari. Misol uchun, Startning ikkita qo'shnisi bor, A va B.

Ushbu qirralarning og'irliklarini qanday ifodalaysiz? Nima uchun boshqa hash jadvalidan foydalanmaslik kerak?

Python

graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2

Golang

graph["start"] = map[string]int{}
graph["start"]["a"] = 6
graph["start"]["b"] = 2

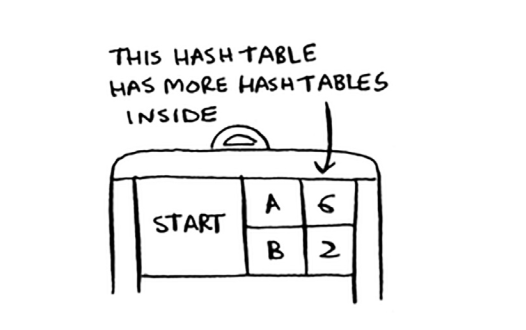
Demak, graph["start"] hash-jadvaldir. Siz barcha qo'shnilarni olishingiz mumkin

Shunday boshlang:

>>> grafikni chop etish ["start"].keys()
["a", "b"]

Boshidan Agacha va boshidan B gacha chekka bor. Agar bu qirralarning og'irliklarini topmoqchi bo'lsangiz-chi?

>>> grafikni chop etish["start"]["a"]
2
>>> grafikni chop etish["start"]["b"]
6

Keling, qolgan tugunlarni va ularning qo'shnilarini grafikga qo'shamiz:

graph["a"] = {}
graph["a"]["fin"] = 1
graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["fin"] = 5
graph["fin"] = {}     <- Tugatish tugunining qo'shnilari yo'q.

To'liq grafik xesh jadvali shunday ko'rinadi.

Keyin har bir tugun uchun xarajatlarni saqlash uchun hash jadvali kerak.

Tugunning narxi bu tugunga boshidan qancha vaqt ketishini anglatadi. Bilasizmi, "Start"dan "B" tuguniga 2 daqiqa ketadi. "A" tuguniga yetib borish uchun 6 daqiqa vaqt ketishini bilasiz (garchi siz kamroq vaqt talab qiladigan yo'lni topishingiz mumkin). Siz tugatishga qancha vaqt ketishini bilmaysiz. Agar siz hali ham narxni bilmasangiz, siz cheksizlikni qo'yasiz. Pythonda cheksizlikni ifodalay olasizmi? Ma'lum bo'lishicha, siz:

infinity = float("inf")

Xarajatlar jadvalini tuzish uchun kod:

infinity = float("inf")
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["fin"] = infinity

Ota-onalar uchun yana bir hash-jadval kerak:

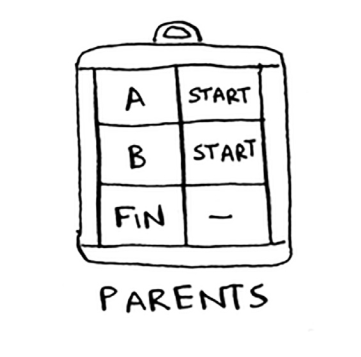
Ota-onalar uchun xesh jadvalini yaratish uchun kod:

Python

parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = None

Golang

parents := make(map[string]string)
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = ""

Va nihoyat, siz qayta ishlagan barcha tugunlarni kuzatib borish uchun massiv kerak, chunki tugunni bir necha marta qayta ishlashingiz shart emas:

Python

processed = []

Golang

processed := []string{}

Hammasi shu. Endi algoritmni ko'rib chiqaylik.

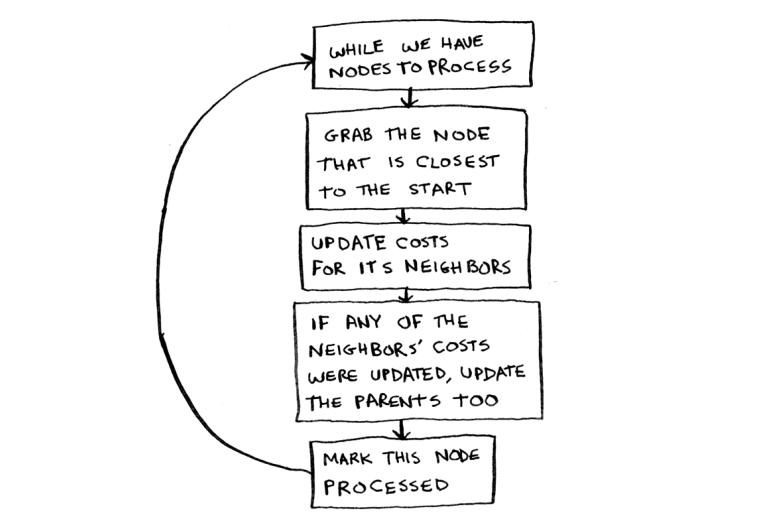
Men sizga avval kodni ko'rsataman va keyin u orqali o'ting. Mana kod:

Python

node = find_lowest_cost_node(costs) # Find the lowest-cost node that you haven't processed yet.
while node is not None: #If you've processed all the nodes, this while loop is done.
    cost = costs[node]
    neighbors = graph[node]
    for n in neighbors.keys(): # Go through all the neighbors of this node.
        new_cost = cost + neighbors[n] # If it’s cheaper to get to this neighbor
        if costs[n] > new_cost: # by going through this node …
            costs[n] = new_cost # … update the cost for this node.
            parents[n] = node # This node becomes the new parent for this neighbor.
    processed.append(node) # Mark the node as processed.
    node = find_lowest_cost_node(costs) # Find the next node to process, and loop.

Golang

node := findLowestCostNode(costs) // Find the lowest-cost node that you haven't processed yet.
for node != "" { // If you've processed all the nodes, this while loop is done.
    cost := costs[node]
    neighbors := graph[node]
    for n := range neighbors { // Go through all the neighbors of this node.
        newCost := cost + neighbors[n] // If it’s cheaper to get to this neighbor
        if costs[n] > newCost { // by going through this node …
            costs[n] = newCost // … update the cost for this node.
            parents[n] = node // This node becomes the new parent for this neighbor.
        }
    }
    processed = append(processed, node) // Mark the node as processed.
    node = findLowestCostNode(costs) // Find the next node to process, and loop.
}

Bu Pythondagi Dijkstra algoritmi! Men sizga funksiya kodini keyinroq ko'rsataman. Birinchidan, ushbu find_lowest_cost_node algoritm kodini amalda ko'rib chiqaylik.

Eng past narxga ega tugunni toping.

Ushbu tugunning narxini va qo'shnilarini oling.

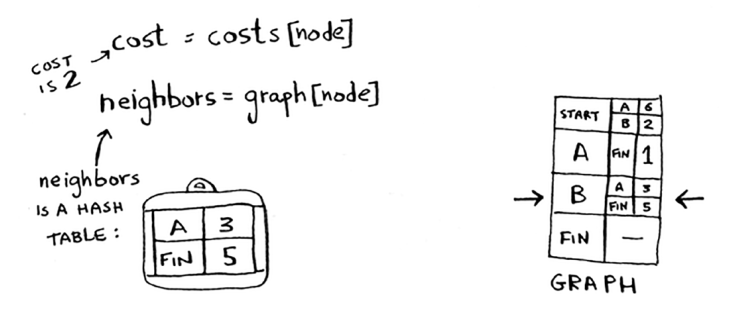
Qo'shnilar orasidan o'ting.

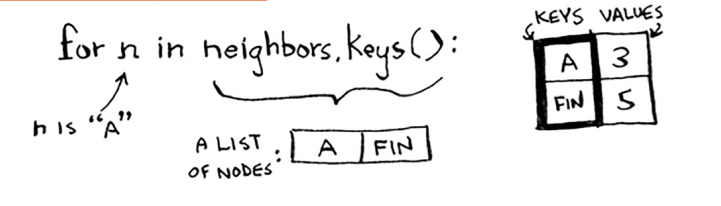
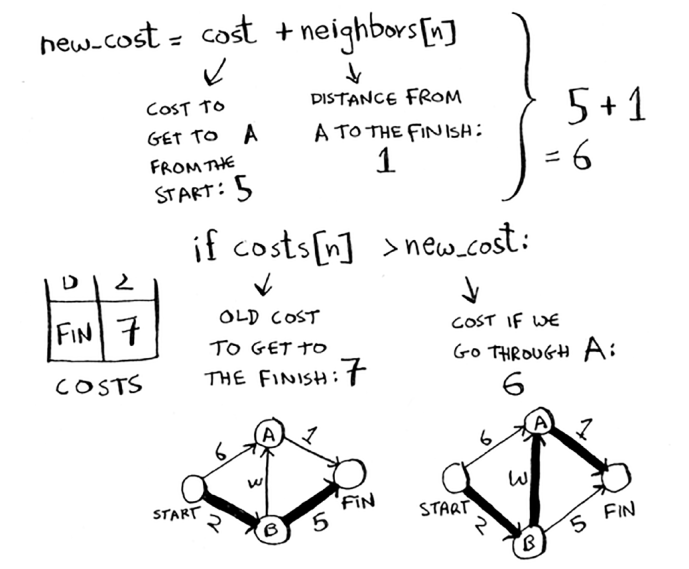
Har bir tugunning narxi bor. Narx - bu tugunga boshidan qancha vaqt ketishi. Bu yerda siz Start > A tugun o'rniga Start > B tugun > A tuguniga o'tsangiz, A tuguniga qancha vaqt ketishini hisoblayapsiz.

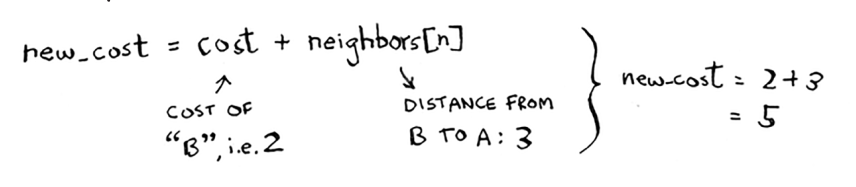
Keling, ushbu xarajatlarni taqqoslaylik.

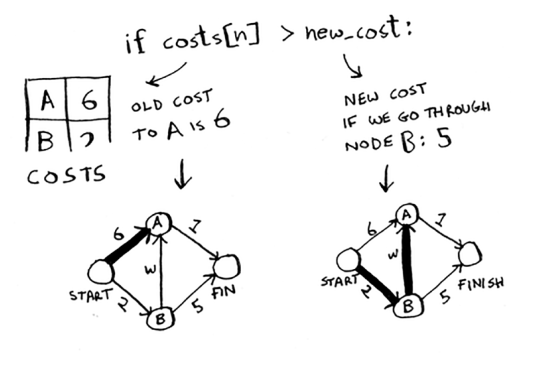
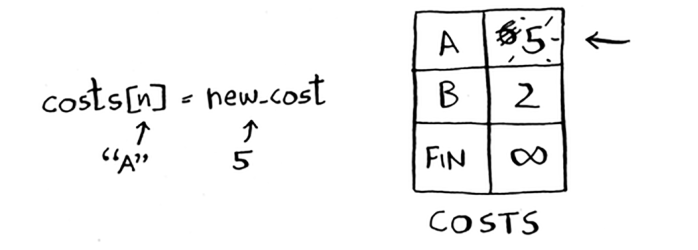
Siz A tuguniga qisqaroq yo'lni topdingiz! Narxni yangilang.

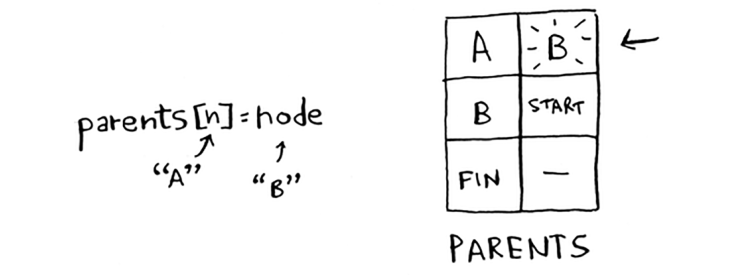
Yangi yo'l B tugunidan o'tadi, shuning uchun B ni yangi ota-ona sifatida belgilang.

OK, siz tsiklning yuqori qismiga qaytdingiz. Keyingi qo'shnisi Finish tugunidir.

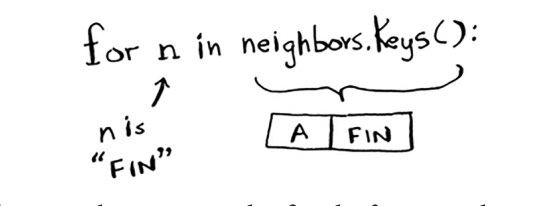
Agar siz B tugunidan o'tsangiz, marraga qancha vaqt ketadi?

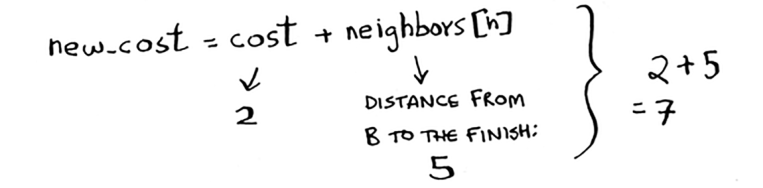
7 daqiqa davom etadi. Oldingi narx cheksiz daqiqalar edi va 7 daqiqa undan kamroq.

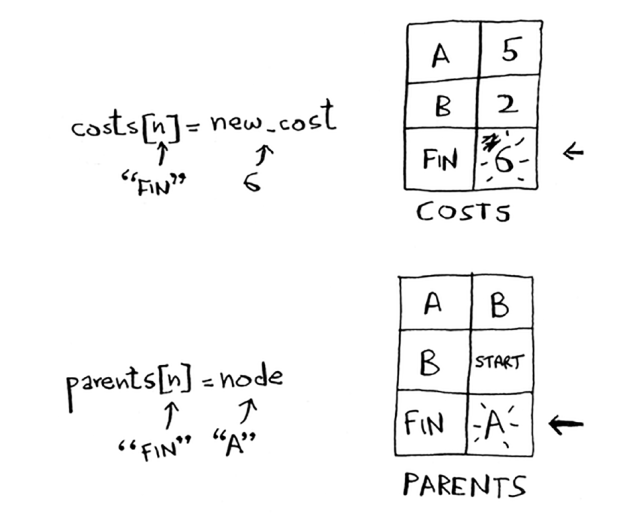
Finish tugunining yangi narxini va yangi ota-onani o'rnating.

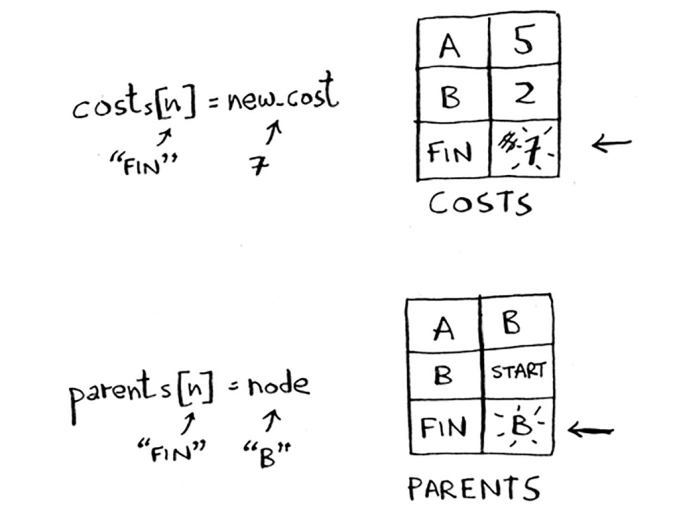
OK, siz B tugunining barcha qoʻshnilari uchun xarajatlarni yangiladingiz. Uni qayta ishlangan deb belgilang.

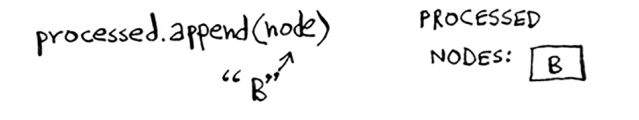
Qayta ishlash uchun keyingi tugunni toping.

A tugunining narxini va qo'shnilarini oling.

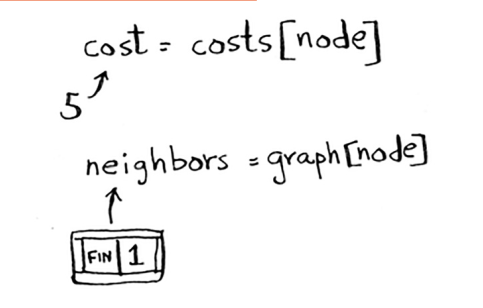
A tugunining faqat bitta qo'shnisi bor: Finish tugun.

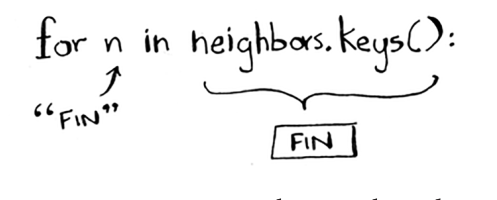
Hozirda Finish tuguniga borish uchun 7 daqiqa vaqt ketadi. Agar siz A tugunidan o'tsangiz, u erga qancha vaqt ketadi?

A tugunidan Finish ga borish tezroq! Narx va ota-onani yangilaymiz.

Barcha tugunlarni qayta ishlaganingizdan so'ng, algoritm tugadi. Umid qilamanki, ko'rsatma sizga algoritmni biroz yaxshiroq tushunishga yordam berdi. find_lowest_cost_node funksiyasi yordamida eng arzon tugunni topish juda oson. Bu kodda:

Python

def find_lowest_cost_node(costs):
    lowest_cost = float("inf")
    lowest_cost_node = None
    for node in costs: # Go through each node.
        cost = costs[node]
        if cost < lowest_cost and node not in processed: # If it's the lowest cost so far and hasn't been processed yet …
            lowest_cost = cost # … set it as the new lowest-cost node.
            lowest_cost_node = node
    return lowest_cost_node

EXERCISES

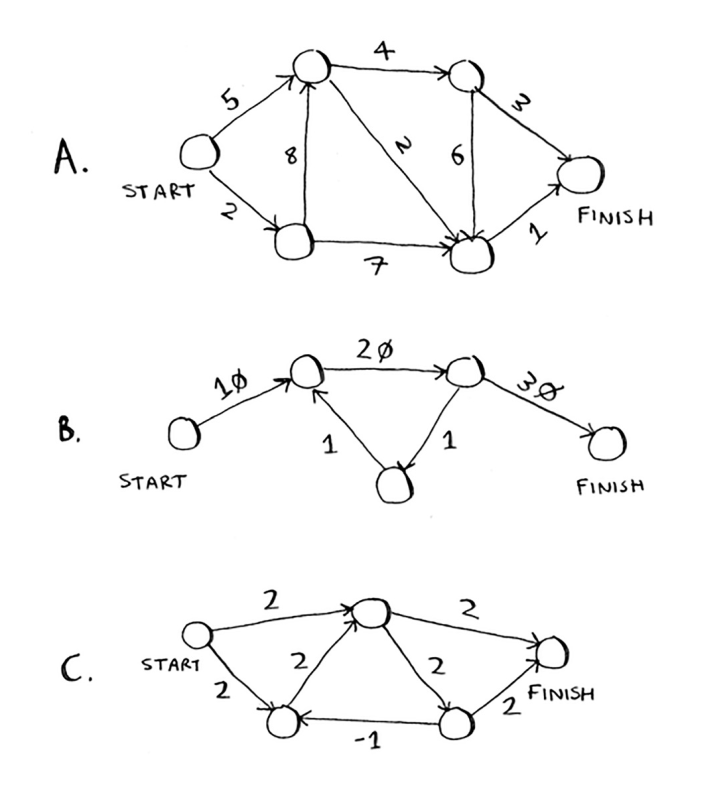
7.1 Ushbu grafiklarning har birida boshidan oxirigacha bo'lgan eng qisqa yo'lning og'irligi qancha?